|
TEMPERATURE ET DENSITE DES GAZ SOLAIRES
keywords = gaz, solar corona, sun, temperature, density, gravity, spicules. mots-clefs = couronne solaire, soleil, gaz, température, densité, gravité, spicules.
Résumé-Essai de compréhension de la température de la couronne solaire par le role de la gravité sur les gaz de diverses densités, et sur les spicules.
|

| La couronne solaire |
![Couronne solaire 1/ 6
TEMPERATURE ET DENSITE DES GAZ SOLAIRES
Résumé : Essai de compréhension de la température de la couronne solaire par le rôle de la gravité
sur les gaz de diverses densités et sur les gaz des spicules. (Adrien Nicco,)
Mots-clés : température - densité - couronne solaire - spicules - vent solaire
Depuis que le gaz à très basse densité constituant la couronne solaire a été étudié et reconnu
se trouver à très haute température , plus de 106 Kelvin, (GROTRIAN 1939), les modèles étudiés
pour interpréter les divers phénomènes liés à cette couronne ont été assez imprécis et discutés :
répartition de la densité gazeuse et de la température avec la distance au soleil, émissions des
rayonnements radio, UV et X, émission et vitesse ou accélération du vent solaire.(ref6).
L'énergie provient évidemment du noyau solaire, mais sa transmission, son maintien dans la
couronne, et ses transformations ne sont pas clairs (ref 1-6). Récemment on a pu affirmer : « pour
une raison encore mal élucidée la chromosphère et la couronne sont plus chaudes que la surface du
soleil » (juillet 2008, ref2a, page 8) ; « bien qu'aucune théorie n'explique encore cette
différence. » (ibid p 9) ; « researchers still do not understand why the temperature rises so much...
over such a small change in radius » ( ? 100 km). (ref 2i).
Quelles sont les conditions physiques possibles dans l'entourage gazeux du soleil ? Peut-on
améliorer cette compréhension ? La masse du soleil détermine la gravité g en fonction de la
distance R au centre du soleil : g = 1,33.1020 / R2 m/s2
Pour R
1 = 696.106 m (surface photosphère), on a : g = 274 m/s2
R
2 = 698.106 m (transition couronne), on a : g = 272 m/s2
R
3 = 1000.106 m (moyenne couronne), on a : g = 133 m/s2
Hypothèse : lorsque le libre parcours moyen des molécules gazeuses devient assez grand,
approchant le rayon de l'astre, par suite de la baisse de la pression en s'éloignant de l'astre, la
gravité retient alors les molécules moins chaudes (moins rapides), ce qui sélectionne dans
l'atmosphère supérieure à très basse pression les molécules plus rapides près de la vitesse de
satellisation, donc à température très élevée. Un flux de fuite dans l'espace s'établit, en relation
avec le flux d'alimentation de cette zone gazeuse très basse pression en atomes très chauds, (ce qui
fournit le vent solaire).
Du côté de la basse couronne, la faible densité en hydrogène a été évaluée autour de
10-9 g/m3, ou 1g/km3 , soit 1014 à 1016 atomes/m3, ou 0,2 à 10.10-9 g/m3 (ref 1 ; 2a). Pour une
température T ? 106 K, l'hydrogène serait atomique H° et largement ionisé H+(+e -). Si on
l'assimile à un gaz parfait on aurait pour R2 = 698.106m près de la transition chromosphérique une
pression p = rT/v pour une mole H° de masse molaire 1 g dans le volume v = 109 m3 à T =106 K :
p2 ? (8,3 j/mol.K).(106K) ? (109 m3/mol ) = 8,3.10-3 Pascal ? 8.10-8 bar.
Du côté de la chromosphère, le même gaz à 8000 K (soit 120 fois moins) serait à pression
assez voisine, car la transition est abrupte, sur moins de 100 km (ref 2i), avec une densité toujours
faible , mais au moins 120 fois plus grande soit 120 g/km3 ou 0,12.10 -6 kg/m3.
v = rT / p = 8,3.8000 / 8,3.10-3 = 8.106 m3 (pour 1 g d'hydrogène atomique)
Alors les parcours libres moyens (L), des atomes près de la transition entre
chromosphère et couronne peuvent être évalués en négligeant le gaz d'électrons.
D'une part en admettant, côté couronne (106 K) , pour 1 g de H, (proton avec un rayon
Couronne solaire 2/ 6
atomique r de 0,01 Å =10-12 m distance d'interaction notable) dans1 km3, alors on calcule :
L = 109/ N ? r2 = 109 m3.g-1 ? (6.1023. 3,14.10-24 m2.g-1) m ? 5.108 m = 500 000 km suffisants pour
faire des parties d'orbite de 4,4.106 km.
D'autre part, en admettant, côté chromosphère (moins de 8000 K), les atomes H° peu
ionisés, avec un rayon admissible d'interaction de 0,5 Å = 0,5.10-10m , soit pour 1 Mole
: L = 8.106 m3.g-1 ? (6.1023 . 3,14 . 0,25 .10-20) m ? 1600 m répartissant l'énergie, mais étant
insuffisant pour la moindre orbite autour du soleil. Or la vitesse orbitale de satellisation V au niveau
de la couronne entre R=700.106 m et R=1000.106 m se situe entre 440 km/s et 360 km/s qui
correspondent à des orbites de 10 000 à 17 000 secondes environ . Ainsi une partie des atomes H+
qui ont des vitesses V de 600 à 360 km/s, c'est à dire une température
T = M.V2 / (6 . 8300) = 7.106 K à 2,6.106 K environ, peuvent orbiter des centaines d'heures sans
retomber sur le soleil, et maintenir la haute température. dans la couronne . Par contre ceux qui ont
une vitesse supérieure à 600 km/s peuvent s ' chapperé et constituer le vent solaire. Il en résulte que
la gravité est assez forte pour retenir sélectivement dans la chromosphère le gaz moins chaud,
et alimenter la couronne en gaz très chaud, créant une transition quasi discontinuité de
densité et température.
Ce flux de gaz très chaud peut être évalué supérieur au flux de vent solaire, lui-même
supérieur au flux de H° probable mesuré au niveau de la terre (ref2h ; 3) de 1 à 4 particules/cm3 à
500-700 km/s qui font globalement 0,25.108 kg/s à 1.108 kg/s dont l'énergie cinétique serait
<.1019 W auxquels on peut ajouter l'énergie potentielle depuis la chromosphère soit <1019 W. Le
total de la puissance consommée par le vent solaire est apparemment ? 1019 W, environ, ce qui
représente moins du millionième de la puissance rayonnée par le soleil P = 3,8.1026 W (constante
solaire). En comparaison, la puissance rayonnée X et UV de longueur d'onde 1 à 100 nm atteint à
peine près de la terre 1 mW/m2 soit globalement 3.1020 W en fond continu, et lors des périodes de
quelques minutes de forte activité 1 à 5 .1023 W (ref1 : fig 2 ; 2f). Ces émissions proviennent
surtout de la chromosphère et de la basse couronne. Les photons X de 1 nm correspondent à
1200 eV soit T ? 5.106 K pour la température d'émission, et les UV de 100 nm d'énergie 12 eV à
T ? 50000 K, températures compatibles avec celles évaluées. D'autre part, la concentration spatiale
du vent solaire recalculée au niveau de la couronne au rayon le plus chaud vers 0,7.106 km serait
(1 à 4 atome/cm 3 ).(150 ?0,7)2 soit 60 000 à 250 000 at/cm3 soit encore 60 à 250.1018 at/km3
ou 0,0001 à 0,00025 g/km3 ; cette densité est une petite fraction de la densité de la couronne,
puisque c'est la fraction qui a l'energie de s'échapper dans l'espace .
Les pressions gazeuses dans l'atmosphère solaire peuvent être calculées en admettant un
équilibre suffisant des gaz et en se basant sur la valeur de 0,008 Pascal calculée pour la basse
couronne. Entre R
2 = 698.106 m et R3 = 1000.106 m pour g autour de 200 m/s2 en négligeant
l'hélium , avec T = 2.106 K on aurait dans la couronne :
Ln (p2 / p3) = ? M(R3 - R2) / (1000.8,3.T) = 200.300.106 / (8300.2.106) ? 3,5 ; d'où p2/p3 = 33. Alors
p
3= 0,008/ 33 = 2,5.10-4 Pa , encore sensible. Ainsi la grande extension de la couronne est possible
grace à la température très élevée, et donc la faible densité, malgré la forte gravité. (De même, pour
la transition ?R=100km, on a p''/p'< 2,2).
D'autre part, du côté chromosphère R2-R1 = 2.106 m et g = 272 m/s2 avec T
moyenne ? 5000 K et M = 1,23 (compte tenu de 25 % d'hélium ). Evaluons p1 photosphère :
Ln(p1/p2) ? 272 . 1,23. 2. 106 ? (8300.5000) ? 16 d'où p1/p2? 9.106. D'où p1 ? 8.10-3. 9.106
? 70000 Pa ? 0,7 bar qui est déjà assez forte pour causer une opacité au delà de 10000 km. de
Couronne solaire 3/ 6
trajet optique (surface de la.photosphère).. La photosphère « en surface » à 5000 K environ aurait
pour 1,23 g (H° et He) un volume v = 8,3 . 5000 / 70000 ? 0,6 m3/mol c'est-à-dire 2,1 g/m3 .
Cette densité est encore faible comparée à 1,4 106 g/m3 moyenne du soleil de rayon R1 ou 100 à
150 .106 g/m3 calculée dans le noyau du soleil. Cependant cette densité approchée est suffisante
pour assurer une opacité optique à travers plus de 20000 km de trajet (à 100 km sous le bord du
disque solaire dans le gaz à près de 5000 K,) ce qui définit le rayon R1 de la photosphère,
observable à 100 km près. En réalité la masse gazeuse présente une continuité d'état du gaz : il n'y
a pas de surface définie de l'astre. Cela est aussi la cause des température et luminance plus faibles
du disque solaire près des bords. En effet la zone centrale du disque comporte une part de
rayonnement émis en profondeur de 100 à 10000 km par du gaz plus chaud que 6000 K ce qui
explique une température moyenne apparente de 5780 K environ par soleil calme.
La question reste posée de l'alimentation en énergie du gaz de la couronne solaire. La
possibilité décrite comporte une contribution mécanique et thermique du gaz de la couche
convective : les granules de la photosphère montrent l'existence de colonnes de convection
fluctuantes de largeur 1000 à 10 000 km , et de profondeur probable au moins 50 000 km (à
200 000 km ?) La température moyenne très hétérogène en profondeur croissant de 6000 à ? 106 K
vers R = 600.106 m environ, ou 2.106 K vers R = 400.106 m ( ref2a), tandis que la pression croîtrait
de p1 = 70 000 Pa, à plus de 109 Pa, la densité croissant de 0,002 kg/m3 à 1 kg/m3 environ. Cette
forte variation de densité avec la profondeur, la pression et la température alimente la convection :
elle peut être modélisée avec une fonction d'état F(p,v,T) difficile à déterminer en laboratoire,
compliquée par la composition du plasma en H°, H+, He (et autres atomes lourds ?) et le
refroidissement par rayonnement près de la photosphère. Il est vraisemblable que des instabilités et
turbulences dans les colonnes de convection apparaissent continuellement causant les éruptions et
sursauts plus ou moins violents, et aussi en permanence sous forme de bulles de 10 à 300 km (?), de
dimension peu visible, qui causent le bouillonnement de la photosphère et de la chromosphère, et
alimente les « spicules » (ref2d) : leur contenu en gaz de température très élevée, grâce à leur
hétérogénéité thermique, peut fournir l'énergie du gaz coronal. Cela représente bien moins de
10-4 fois la puissance rayonnée globalement par le soleil (difficile à distinguer par spectroscopie).
Les « ondes de Moreton » ainsi que les manifestations électromagnétiques « ondes
d'Alfven » leur sont sans doute liées et partagent une part du transport d'énergie dont l'évaluation
reste à préciser (ref4 ;5). D'autres mécanismes hypothétiques pourraient intervenir par
l'intermédiaire de particules fondamentales exotiques (ref 1)..
Dans le cas de l'atmosphère terrestre, entre 10 et 110 km d'altitude (M = 28,8 g/mol et
T = 200 K en moyenne) la pression chute de 0,25 .105 Pa à 10-3 Pa. Au dessus de 160 km avec T
autour de 600 K l'hydrogène devient important, surtout H° et H2 , mais le libre parcours
moléculaire reste limité (quelques km ?). En fait l'hydrogène provient surtout du vent solaire et les
H+ peuvent être encore présents après le piégeage magnétique terrestre : les molécules de vitesse
supérieure à 7,8 km/s sont partiellement satellisables (ceinture de VanAllen); leur température
serait : T = M . V2 / (6 .8,3) soit 1200 à 2400 K. Des mesures de 600 à 700 K ont été observées
au dessus de 160 km par soleil calme, mais par soleil actif le flux solaire a permis d'observer 1200 à
1800 K à grande hauteur ce qui est assez compatible avec le piégeage du gaz par la gravité.
En conclusion, le rôle de la gravité sur l'atmosphère solaire semble être essentiel pour
comprendre le niveau de température de la couronne solaire, sa permanence, la densité
gazeuse en altitude et l'alimentation du vent solaire. De même les températures terrestres à
l'altitude de 100 à 200 km peuvent être dépendantes de ce mécanisme, qui doit affecter
naturellement les hautes atmosphères des astres de gravité assez forte (Vénus, Jupiter).
NICCO . A. - Dolus - 16/08/2008 -5/08/2009.
Couronne solaire 4/ 6
ADDITIF 2011- Les publications récentes de De Pontieu et al (Science2011,DOI..10.1126/)
(Science .11974738/) ainsi que Nancy Atkinson (ref 7)(Previously unseen Plasma Jets ; Universe
Today, Jan 6 2011) http://www.universetoday.com/82266/previously-unseen-super-hot-plasma-jetsheat-the-suns-corona/ paraissent en accord avec les évaluations faites suivant les hypothèses
présentées. De même les études spectroscopiques très nombreuses ont montré que les répartitions de
rayonnements et de températures détectent difficilement la faible fraction de molécules très chaudes
dans les jets (spicules) du bouillonnement permanent, mais paraissent cohérentes avec le
mécanisme de sélection par la gravité (Klaus Wilhelm et al, Space Rev (2007)133 : 103-179 ;( DOI
10.1007/s 11214-007-9285-0). Des vues du soleil prises avec la raie de l'hydrogène ,suite à des
éruptions, semblent montrer des phases d'enrichissement de la couronne controlées par la gravité
suivant l'hypothèse décrite qui invoque la satellisation individuelle de particules du gaz. :
photographie par le satellite SOHO ? (ref6).Le rôle primordial de la gravité dans la selection et
la satellisation des particules très chaudes paraît bien être essentiel. D'autre part, les champs
magnetiques solaires doivent causer une organisation du mouvement des H+ et des e- ,qui
retombent en continu sur le soleil, après leur projection par le bouillonnement permanent . Ainsi les
pôles solaires, et les taches sombres lors des periodes plus actives, montreraient une température
plus basse, par suite d'un flux retombant partiellement refroidi par rayonnement. En outre les
charges electriques de ce flux retombant voient leurs trajectoires spiraler dans le sens qui accroit le
champ magnétique et ralentit la chute . D'autre part il est normal que les particules qui sont à des
distances croissantes de l'astre soient sélectionnées avec des énergies, des vitesses supérieures, ce
qui concorde avec les observations du vent solaire qui semble « accélèrer » en s'éloignant de
l'astre : le flux global doit diminuer avec l'éloignement du soleil par suite de la sélection
énergétique.
NICCO . A --Béthune-21/5/2011. Voir aussi Ref 8 ; 2013.
REFERENCES
(1) K. ZIOUTAS - Courier CERN juin 2008-48 (19-21) (et autres citations)
http://cerncourier.com/cws/article/cern/34259
(2) Internet-WIKIPEDIA
(a) soleil ; (b) photosphère ; (c) rayonnement ; (d) chromosphère ; (e) couronne solaire ;
(f) éruption solaire ; (g) sursaut solaire ; (h) vent solaire ; (i) transition région; spicules.
(3) http://www.swpc.noaa.gov/ace/mag_swepam_24h.html' target=?
(4) http://solar.physics.montana.edu/nuggets/2002/O2O2O8.html
(5) DB Jess et al 2009 Science 323 ,1582
(6) http://system.solaire.free.fr/soleil.htm
(7) http://www.universetoday.com/82266/previously-unseen-super-hot-plasma-jets-heat-thesuns-corona/
(8) Wikipedia Couronne solaire,2013, http://fr.wikipedia.org/wiki/Couronne_solaire Ref M.Vail
http://www.journaldelascience.fr/espace/articles/soleil-mystere-chauffage-coronal-passe-detreresolu-3280 Ces travaux ont été publiés le 2 octobre 2013 dans la revue The Astrophysical Journal
sous le titre « Observational Quantification of the Energy Dissipated by Alfvén Waves in a Polar
Coronal Hole: Evidence that Waves Drive the Fast Solar Wind »(arXiv:1204.5809.v1..26Apr2012)
Couronne solaire 5/ 6
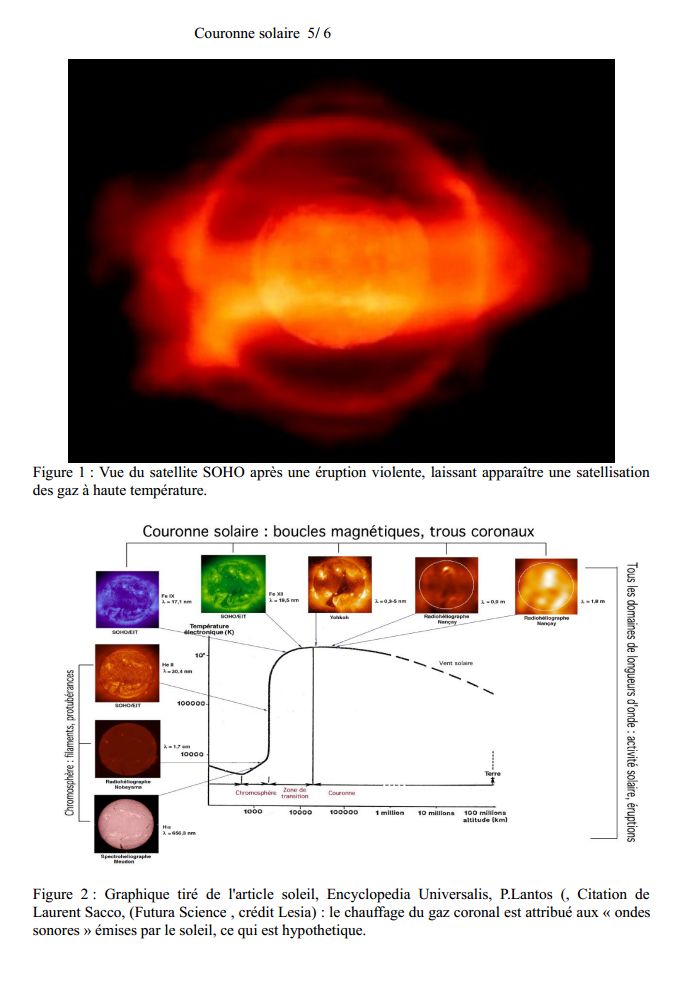
Figure 1 : Vue du satellite SOHO après une éruption violente, laissant apparaître une satellisation
des gaz à haute température.
Figure 2 : Graphique tiré de l'article soleil, Encyclopedia Universalis, P.Lantos (, Citation de
Laurent Sacco, (Futura Science , crédit Lesia) : le chauffage du gaz coronal est attribué aux « ondes
sonores » émises par le soleil, ce qui est hypothetique.
Couronne solaire 6/ 6
Références récentes
http://www.huffingtonpost.fr/2015/02/14/soleil-nasa-espace-video_n_6683040.html?
utm_hp_ref=fr-science vues d'éruptions etc remarquables ; seconde video avec vue continue du
soleil ; peu de commentaire !
http://www.nature.com/nature/journal/v522/n7555/full/nature14478.html Interpretation du
transport d'energie à la couronne solaire par les champs magnetiques emergeant de la surface
solaire. Température et densité avec la distance au soleil (en accord).
Small-scale dynamo magnetism as the driver for heating the solar atmosphere
Tahar Amari, Jean-François Luciani & Jean-Jacques Aly Affiliations Contributions Corresponding
author Nature 522, 188-191 (11 June 2015) doi:10.1038/nature14478 Received 20 December 2014/
Accepted 15 April 2015/ Published online 10 June 2015 (l'interprétation de l'absorption de l'energie
à très haute température reste incompréhensible. N.A.)
https://en.wikipedia.org/wiki/Corona description et discussion de quelques interprétations ;
en fin des jets très chauds sont cités comme alimentant la couronne. Références précisant l'existence
de « nanojets » aptes à fournir la haute température ?, sans expliquer la transition rapide. Voir :
http://www.rediff.com/news/slide-show/slide-show-1-mystery-of-suns-hot-outeratmosphere-solved/20110107.htm ainsi que
http://www.rediff.com/news/slide-show/slide-show-1-mystery-of-suns-hot-outeratmosphere-solved/20110107.htm#3
http://www.nature.com/nature/journal/v475/n7357/abs/nature10235.html Essai de
comprehension de la température de la couronne solaire. Références Depontieu.
http://www.universetoday.com/82266/previously-unseen-super-hot-plasma-jets-heat-thesuns-corona/ Nancy Atkinson : Observations peu explicites , et discussions vagues.
De Pontieu, B. et al. The origin of hot coronal plasma. Science 331, 55-58 (2011)
De Pontieu, B., McIntosh, S. W., Hansteen, V. H. & Schrijver, C. J. Observing the roots of solar
coronal heating-in the chromosphere. Astrophys. J. 701, L1-L6 (2009)
https://arxiv.org/pdf/1606.06132 de C Beck - 2016- · R. Rezaei2 · K. G. Puschmann3 ·
Fabbian4,5,6D. Solar Physics.arXiv:1606.06132v1 [astro-ph.SR] 20Jun2016. DOI: 10.1007/.....
-Spectroscopy at the solar lib: II. Spectroscopy at the solar limb: II. Are spicules heated to coronal
temperature ?
SPACE REVIEWS Space Sci Rev (2007) 133: 103-179 DOI 10.1007/s11214-007-9285-0
Observations of the Sun at Vacuum-Ultraviolet Part II: Results and Interpretation
Klaus Wilhelm · Eckart Marsch · Bhola N. Dwivedi · Uri Feldman
. Received: 22 February 2007 / Accepted: 9 October 2007 / Published online: 9 January 2008
© Springer Science+Business Media B.V. 2008 . (Article revue très détaillé, mais sans
interprétation des très hautes températures 10^6 °K. N.A.)
Suite aux aux remarques sur la temperature de la couronne solaire et à l'absence d'explication sur
l'absorption d'energie qui procure cette temperature., l'article récent Bertolucci et al 2017
DarkUniverse 17, 13 .cité par Courrier CERN octo 2017 reprend:
'The origin of solar flares, powerful bursts of radiation appearing as sudden flashes of light, has
puzzled astrophysicists for more than a century. The temperature of the Sun's corona measuring
several times hotter than its surface, is also a long standing enigma.'. (L'article avance une raison
invoquant un flux spatial anisotrope de matière noire spatiale pouvant être une cause de ces
émissions solaires irrégulières. Cependant l'absorption intense de particules 'wimps' ou autres par
le gaz coronal n'est pas compréhensible. N.A.)](image_049.gif)